Inleiding tot vermenigvuldiging en vermenigvuldigingstabellen
In een vroeger tijdperk was het een groot probleem om grotere getallen toe te voegen. De wiskundige ontdekt een nieuwe techniek om op een snelle manier een groter aantal waarden toe te voegen. In dit artikel hebben we een nieuwe techniek geïntroduceerd om dezelfde getallen op te tellen. We zullen ook enkele methoden gebruiken om de methoden in detail te illustreren.
Wat is vermenigvuldigen?
Vermenigvuldigen is de snelste manier om getallen toe te voegen. Er zijn verschillende methoden en symbolen om vermenigvuldiging weer te geven. We gebruiken de tekens (*), (.) en (x) tussen twee getallen voor vermenigvuldiging.
Laat a en b twee willekeurige getallen zijn, dan wordt de vermenigvuldiging weergegeven door
A . B
een * b
bijl
Soorten vermenigvuldiging
Er zijn verschillende manieren om te vermenigvuldigen. Docenten dringen er soms op aan om een bepaalde aanpak in de klas te gebruiken, maar het is van cruciaal belang dat elke leerling een vermenigvuldigingsstrategie vindt die bij hem of haar past.
Hoewel bepaalde benaderingen meer geschikt zijn voor specifieke soorten problemen, kunnen alle vermenigvuldigingsmethoden worden gebruikt om elk vermenigvuldigingsprobleem correct te beantwoorden.
Toevoegingsmethode:
Lange vermenigvuldigingsmethode
Lijnen tekenen
We zullen elk type één voor één bespreken met gedetailleerde voorbeelden.
1. Toevoegingsmethode:
In een methode voegen we hetzelfde getal op zichzelf toe door een specifiek getal. 13*5 betekent bijvoorbeeld dat we 13 zelf 5 keer moeten optellen.
13 * 5 = 13 + 13 + 13 + 13 + 13 = 65
Deze methode is erg handig als je te maken hebt met kleine getallen of grotere getallen met kleine optellingen. Maar de methode is zeer ontroerend als we een groter getal kiezen, zoals 64 * 598. Het betekent dat we 64 bij 598 keer hebben toegevoegd.
2. Lange vermenigvuldigingsmethode
Lange vermenigvuldiging is een traditionele manier van vermenigvuldigen. De meesten van ons leren op schoolniveau over de vermenigvuldiging van twee of meer twee getallen. Als we eenmaal het concept van de grotere vermenigvuldiging begrijpen, wordt de fout van een vergissing klein.
598 * 64
Delen van de lange vermenigvuldigingsmethode
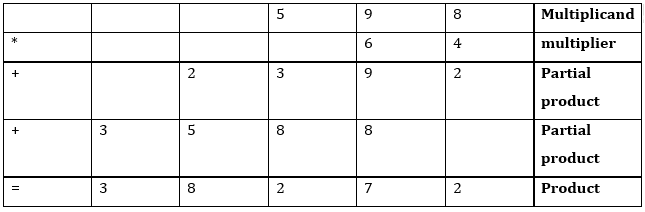
We volgen enkele stappen om te vermenigvuldigen:
• Eerst schrijven we een getal bovenaan en 2de onderaan. We moeten de getallen rangschikken met betrekking tot plaatswaarden. We hebben er een gewoonte van gemaakt om een groot getal op de bovenste regel te schrijven.
• We beginnen te vermenigvuldigen met het onderste eenmalig plaatswaardecijfer naar de bovenste 1e plaatswaarde.
• Als het antwoord groter is dan 9 dan schrijven we de waarde van de 1e plaats en nemen de waarde van de tientallen mee naar de waarde van de 2e plaats van het bovenste getal.
• Als het getal kleiner is dan en gelijk is aan 9 schrijven we het getal gewoon.
• Procedure loopt van rechts naar links.
• Als het cijfer van de 1e plaats wordt vermenigvuldigd met elke waarde tot de bovenste waarde, moeten we naar het nummer van de 2e plaats gaan.
• Schrijf deze keer je antwoorden in een nieuwe rij en schuif de plaats van één cijfer naar links.
• Als de vermenigvuldiging is beëindigd, hebben we op de laatste regel alle bijbehorende waarden opgeteld.
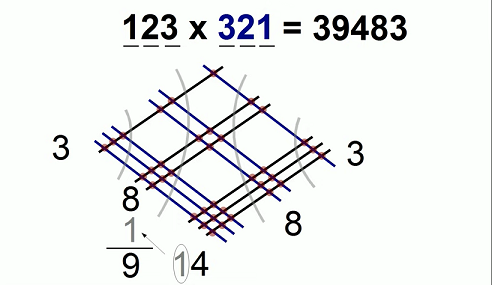
3. Lijnen tekenen
De methode staat bekend als de Japanse lijnvermenigvuldigingsmethode. Dit is de visuele weergave van vermenigvuldiging.
Laten we 123 * 321 = 39483 vermenigvuldigen
Dit is een weergave in het onderste diagram.
Wat is de tafel van vermenigvuldiging?
Een tafel van vermenigvuldiging is een groep van vermenigvuldiging van een bepaald getal. Meestal is het van 2 tot 12.
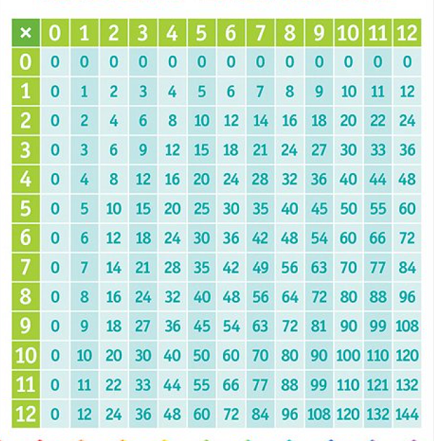
De mondelinge tafel speelt een belangrijke rol bij het gemakkelijk begrijpen en oplossen van de vermenigvuldigingsmethode.
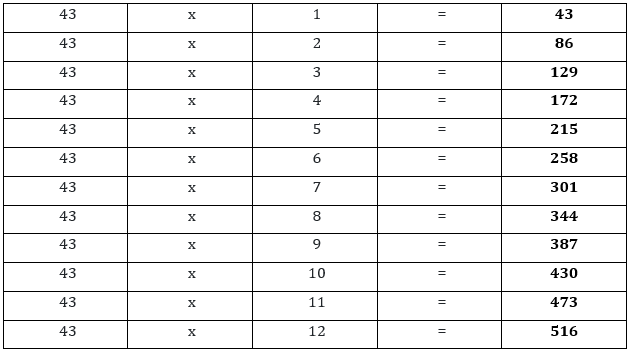
Kinderen kunnen een tafel van vermenigvuldiging voor het leren van maaltabellen en factoren van het getal. De tafel van vermenigvuldiging speelt een cruciale rol in de ontwikkeling van de vroege opvoeding van het kind.
Plezier met de tafel van vermenigvuldiging
De tafel van 9 is erg genietend vol voor de studenten om op de toetspagina te schrijven.
Schrijf het tellen van 0 tot 9 van boven naar beneden en dan van onder naar boven 0 tot 9 wanneer je onze volledige tabel hebt.

Veelgestelde Vragen / FAQ
1. Wat is vermenigvuldigen en hoe verschilt het van optellen en aftrekken?
Vermenigvuldigen is een wiskundige bewerking waarbij gelijke groepen of reeksen getallen worden gecombineerd om een totaal te vinden. Het verschilt van optellen doordat het herhaaldelijk optellen van hetzelfde getal inhoudt, en van aftrekken doordat het gaat om het vinden van een product in plaats van een verschil.
2. Wat zijn de basistafels van vermenigvuldiging en hoe kunnen ze worden onthouden?
De basistafels van vermenigvuldiging zijn de reeksen getallen van 1 tot 10, en ze kunnen worden onthouden door herhaling en oefening. Er zijn veel technieken en strategieën die kunnen worden gebruikt om het onthouden effectiever en boeiender te maken, zoals het gebruik van flashcards, liedjes of spelletjes.
3. Wat zijn enkele veelvoorkomende fouten die kinderen maken bij het leren van vermenigvuldigen, en hoe kunnen ze worden vermeden?
Veelgemaakte fouten die kinderen maken bij het leren van vermenigvuldigen, zijn onder meer het verwarren van vermenigvuldigen met optellen of aftrekken, het vergeten van de volgorde van bewerkingen en het verkeerd tellen of overslaan van getallen in de tafel van vermenigvuldiging. Deze fouten kunnen worden vermeden door de verschillen tussen bewerkingen te benadrukken, de volgorde van bewerkingen te oefenen en visuele hulpmiddelen te gebruiken om te helpen bij het tellen en onthouden.
4. Hoe kunnen ouders en leerkrachten leren vermenigvuldigen aantrekkelijker en leuker maken voor kinderen?
Leren vermenigvuldigen kan voor kinderen aantrekkelijker en leuker worden gemaakt door gebruik te maken van verschillende leermethoden, zoals spelletjes, puzzels en manipulatieve middelen. Real-world toepassingen van vermenigvuldiging, zoals het berekenen van recepten of het meten van ingrediënten, kunnen ook worden gebruikt om het praktische gebruik van deze vaardigheid te demonstreren en de motivatie te vergroten.
5. Wat zijn enkele praktische toepassingen van vermenigvuldiging en waarom is het belangrijk dat kinderen deze vaardigheid leren?
Vermenigvuldigen is een belangrijke vaardigheid die kinderen moeten leren, omdat het op veel gebieden van het leven wordt gebruikt, waaronder wetenschap, techniek en financiën. Het is nodig voor basisberekeningen zoals het bepalen van de kosten van artikelen, het berekenen van wisselgeld en het bepalen van afstand of snelheid. Beheersing van vermenigvuldiging kan ook het algehele wiskundige vermogen en probleemoplossende vaardigheden verbeteren.
Samengevat
In dit bericht hebben we de methode van vermenigvuldiging geleerd en enkele tabellen als voorbeeld met een truc met een rommelbit om ze te onthouden. Nu kun je tabellen leren en ze gebruiken om vermenigvuldigingsproblemen op te lossen.